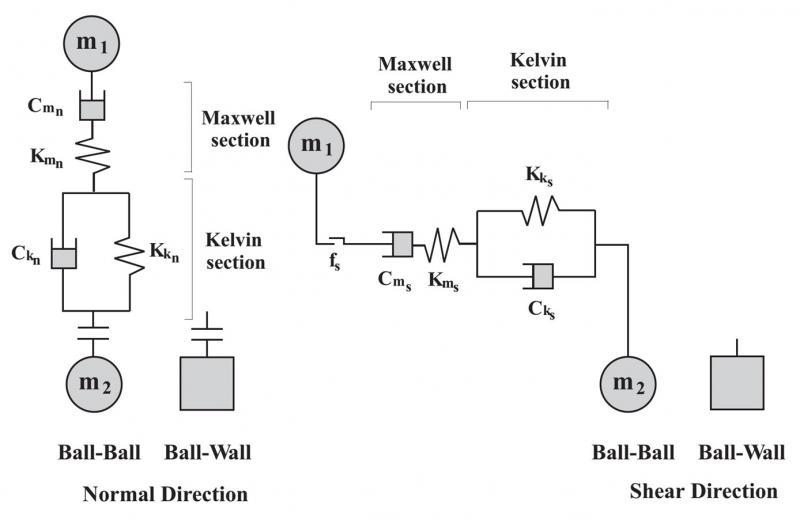
Secure cookies are created on the Website if you are logged into, or choose to log into, your Google account and choose to view an embedded YouTube video or similarly available Google Service on the Website. These are third-party cookies which ITASCA has no control over.
Name: NID
Description: Used by Google to store user preferences and information for signed-out users, such as language settings, search result preferences, and SafeSearch settings. It assigns a unique ID to a user's browser, enabling Google to personalize user experience and provide relevant advertising data to businesses using Google Ads.
Provider: .google.com
Expiry: 6 months
Name: HSID
Description: This cookie is a security measure used by Google to authenticate users and protect their data. It stores digitally signed and encrypted records of a user's Google account ID and the timestamp of their most recent sign-in. This cookie works in conjunction with the SID cookie to verify user identity and prevent unauthorized access to Google services.
Provider: .google.com
Expiry: 2 years
Name: SAPISID
Description: A security cookie used to store user preferences and enable personalized features across Google services, including advertising. SAPISID stores user preferences, such as language settings, the number of search results to display, and whether the SafeSearch filter is enabled.
Provider: .google.com
Expiry: 2 years
Name: SID
Description: A security cookie used by Google to identify a user's Google Account and their most recent sign-in time. It's paired with other cookies like HSID to help protect against attacks like cross-site request forgery, ensuring that requests within a browsing session are made by the user and not by malicious third-party sites.
Provider: .google.com
Expiry: 2 years
Name: SIDCC
Description: The primary function of SIDCC is to act as a security measure, ensuring the protection of user data on Google sites and services. Google uses SIDCC to identify trusted web traffic, helping to distinguish legitimate user activity from potentially malicious attempts to access accounts or data.
Provider: .google.com
Expiry: Up to 1 year
Name: SSID
Description: Primarily used for security and personalization in relation to YouTube videos and Google's advertising services. The SSID cookie is set when a user interacts with a YouTube video player. It's a long-lasting cookie, with a typical expiration time of two years. While it's used for personalization, it also plays a role in preventing fraud and ensuring a secure browsing experience. Users can manage their cookie settings in their browser to control how Google uses this cookie and others.
Provider: .google.com
Expiry: 2 years
Name: APISID
Description: A security cookie used by Google, particularly in relation to YouTube and other services. It plays a role in personalizing ads by collecting user information based on recent searches and interactions. This allows Google to display targeted advertisements that are more relevant to a user's interests.
Provider: .google.com
Expiry: 6 months
Name: __Secure-1PAPISID
Description: A secure, persistent cookie used by Google to store information about your interactions with Google services and ads (including Google Search and YouTube).
Provider: .google.com
Expiry: 2 years
Name: __Secure-1PSID
Description: Used for targeting purposes, specifically to build a profile of website visitor interests to show relevant and personalized Google advertising. It is placed on every page of a website using Google services, including Google's own sites, and is used regardless of whether you are logged into your Google account.
Provider: .google.com
Expiry: Up to 2 years
Name: __Secure-1PSIDCC
Description: Used for targeting purposes, specifically to build a profile of website visitor interests to show relevant and personalized Google advertising. It's a first-party cookie, meaning it's set by Google directly when you visit Google properties or sites that use Google services. This cookie helps Google tailor ads to your preferences based on your browsing activity. It is placed on every page of a website using Google services, including Google's own sites, and is used regardless of whether you are logged into your Google account.
Provider: .google.com
Expiry: 12 months
Name: __Secure-1PSIDTS
Description: Primarily used for targeting and personalized advertising. It helps Google build a profile of a website visitor's interests, allowing them to display relevant ads based on those interests. This cookie is set by Google and is placed on pages where Google services or advertising is present.
Provider: .google.com
Expiry: 6 months
Name: __Secure-3PAPISID
Description: Third-party cookie used by Google to track users and build a profile of their browsing interests, primarily for the purpose of delivering personalized and relevant advertising. It is considered a tracking cookie because it follows users across different websites.
Provider: .google.com
Expiry: 2 years
Name: __Secure-3PSID
Description: Third-party cookie set by Google and is used to track users across different websites for advertising purposes.
Provider: .google.com
Expiry: 2 years
Name: __Secure-3PSIDCC
Description: A security and authentication cookie used by Google, primarily for retargeting and ad personalization. It helps build a profile of website visitor interests to show more relevant ads. It is also used for security purposes, including protecting user data and preventing fraud.
Provider: .google.com
Expiry: 1 year
Name: __Secure-3PSIDTS
Description: Used to collect information about user interactions with Google services and ads, including websites and apps, to personalize ads and measure advertising effectiveness. It's a unique identifier that helps Google build a profile of user interests for targeted advertising.
Provider: .google.com
Expiry: 1 year